https://www.blogger.com/follow.g?view=FOLLOW&blogID=4060652467429149727
INTRODUCTION TO TAGUCHI METHOD
Optimization of process parameters
is done to have great control over quality, productivity and cost aspects of
the process. Off-line quality control is considered to be an effective approach
to improve product quality at a relatively low cost. Analysis of variance
(ANOVA) is used to study the effect of process parameters on the machining
process. The approach is based on Taguchi method, the signal-to-noise (S/N)
ratio and the analysis of variance (ANOVA) are employed to study the
performance characteristics.
Introduction
Taguchi methods are statistical
methods developed by Genichi Taguchi to improve the quality of
manufactured goods and more recently
also applied to engineering (Rosa et al. 2009), biotechnology (Rao et al. 2008,
Rao et al. 2004), marketing and advertising (Selden 1997). Professional
statisticians have welcomed the goals and improvements brought about by Taguchi
methods, particularly by Taguchi's development of designs for studying
variation. After World War II, the Japanese manufacturers were struggling to
survive with very limited resources. If it were not for the advancements of
Taguchi the country might not have stayed afloat let alone flourish as it has.
Taguchi revolutionized the manufacturing process in Japan through cost savings.
He understood, like many other engineers, that all manufacturing processes are
affected by outside influences, noise. However, Taguchi realized methods of
identifying those noise sources, which have the greatest effects on product
variability. His ideas have been adopted by successful manufacturers around the
globe because of their results in creating superior production processes at
much lower costs.The enemy of mass production is variability. Success in
reducing it will invariably simplify processes, reduce scrap, and lower costs”
(Box and Bisgaard 1988). The main
objective in the Taguchi
method is to design robust systems
that are reliable under uncontrollable conditions (Taguchi1978,
Byrne1987 and Phadke1989).The method
aims to adjust the design parameters (known as the controfactors) to their
optimal levels, such that the system response is robust – that is, insensitive
to noise factors, which are hard or impossible to control (Phadke1989). In the
1980s Genichi Taguchi (1985; 1986; 1993) received international attention for
his ideas on variation reduction, starting with the translation of his work
published in Taguchi and Wu (1979).
Process Optimization
Process optimization is the
discipline of adjusting a process to optimize some specified set of parameters without violating some constraint.
The most common goals are minimizing cost, maximizing throughout, and/or
efficiency. This is one of the major quantitative tools in industrial decision-making.
When optimizing a process, the goal is to maximize one or more of the process specifications,
while keeping all others within their constraints. Process Optimization Tools Many
relate process optimization directly to use of statistical techniques to
identify the optimum solution. This is not true. Statistical techniques are
definitely needed. However, a thorough understanding of the process is required
prior to committing time to optimize it. Over the years, many methodologies
have been developed for process optimization including Taguchi method, six sigma,
lean manufacturing and others. All of these begin by an exercise to create the
process map.
Taguchi’s method:
Taguchi's techniques have been used
widely in engineering design (Ross 1996 & Phadke 1989). The Taguchi method
contains system design, parameter design, and tolerance design procedures to achieve
a robust process and result for the best product quality (Taguchi 1987 &
1993). The main trust of Taguchi's techniques is the use of parameter design
(Ealey Lance A.1994), which is an engineering method for product or process
design that focuses on determining the parameter (factor) settings producing
the best levels of a quality characteristic (performance measure) with minimum
variation. Taguchi designs provide a powerful and efficient method for
designing processes that operate consistently and optimally over a variety of
conditions. To determine the best design, it requires the use of a
strategically designed experiment, which exposes the process to various levels
of design parameters. Experimental design methods were developed in the early
years of 20th century and have been extensively studied by statisticians since
then, but they were not easy to use by practitioners (Phadke 1989). Taguchi's
approach to design of experiments is easy to be adopted and applied for users
with limited knowledge of statistics; hence it has gained a wide popularity in
the engineering and scientific community. Taguchi specified three situations:
Larger the better (for example,
agricultural yield); Smaller the better (for example, carbon dioxide
emissions); and On-target, minimum-variation (for example, a mating part in an
assembly).
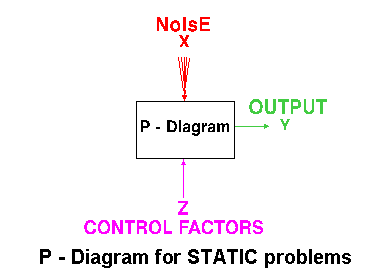
P
Diagram
Taguchi has used Signal-Noise (S/N)
ratio as the quality characteristic of choice. S/N ratio is used as
measurable value instead of standard
deviation due to the fact that, as the mean decreases, the
standard deviation also deceases and
vice versa.
Contributions of Taguchi Methods:
Taguchi has made a very influential
contribution to industrial statistics. Key elements of his quality
philosophy include the following:
Taguchi loss function (Ross 1996):
used to measure financial loss to society resulting from poor
quality;
The philosophy of off-line quality
control (Logothetis and Wynn 1989): designing products and
processes so that they are
insensitive ("robust") to parameters outside the design engineer's
control;
and Innovations in the statistical
design of experiments: Atkinson, Donev, and Tobias, (2007), notably
the use of an outer array for
factors that are uncontrollable in real life, but are systematically varied in
the experiment. Taguchi proposed a
standard 8-step procedure for applying his method for
optimizing any process.
Taguchi's Rule for Manufacturing:
Taguchi realized that the best
opportunity to eliminate variation is during the design of a product and
its manufacturing process.
Consequently, he developed a strategy for quality engineering that can be
used in both contexts. The process
has three stages:
I. System design
II. Parameter design
III. Tolerance design
System design
This is design at the conceptual
level, involving creativity and innovation.
Parameter design
Once the concept is established, the
nominal values of the various dimensions and design parameters
need to be set, the detail design
phase of conventional engineering. This is sometimes called
robustification.
Tolerance design
With a successfully completed
parameter design, and an understanding of the effect that the various
parameters have on performance,
resources can be focused on reducing and controlling variation in the
critical few dimensions.
Eight-Steps in Taguchi Methodology:
Step-1: Identify the main function,
side effects, and failure mode
Step-2: Identify the noise factors,
testing conditions, and quality characteristics
Step-3: Identify the objective
function to be optimized
Step-4: Identify the control factors
and their levels
Step-5: Select the orthogonal array
matrix experiment
Step-6: Conduct the matrix
experiment
Step-7: Analyze the data, predict
the optimum levels and performance
Step-8: Perform the verification
experiment and plan the future action
Methodology Used: Taguchi Techniques
Dr. Taguchi's Signal-to-Noise ratios
(S/N), which are log functions is based on “ORTHOGONAL
ARRAY” experiments which gives much
reduced “variance” for the experiment with “optimum
settings “of control parameters.
Thus the marriage of Design of Experiments with optimization of
control parameters to obtain BEST
results is achieved in the Taguchi Method. "Orthogonal Arrays"
(OA) provide a set of well balanced
(minimum)experiments & desired output, serve as objective
functions for optimization, help in
data analysis and prediction of optimum results.
Mathematical modeling:
“ORTHOGONAL
ARRAYS “(OAs) experiments
Using OAs significantly reduces the
number of experimental configurations to be studied
Montgomery, (1991). The effect of
many different parameters on the performance characteristic in a
process can be examined by using the
orthogonal array experimental design proposed by Taguchi.
Once the parameters affecting a
process that can be controlled have been determined, the levels at
which these parameters should be
varied must be determined. Determining what levels of a variable
to test requires an in-depth
understanding of the process, including the minimum, maximum, and
Shyam Kumar Karna & Rajeshwar
Sahai
15
current value of the parameter. If
the difference between the minimum and maximum value of a
parameter is large, the values being
tested can be further apart or more values can be tested. If the
range of a parameter is small, then
less value can be tested or the values tested can be closer together.
The Taguchi method is a powerful
tool for designing high quality systems. To increase the experimental
efficiency, the L18 mixed orthogonal table in the Taguchi quality design. Ross (1988)
is used to determine the significant
machining factors. In the experiments, we select six influential machining parameters, such as cutting tools of
different materials, depth of cut, cutting speed, feed rate, working temperature and ultrasonic
power, each of which has three different levels (high, medium and low levels).
Design of Experiment (Doe's)
Requires Planning:
I. Design and Communicate the
Objective:
II. Define the Process:
III. Select a Response and
Measurement System:
IV. Ensure that the Measurement
System is Adequate:
V. Select Factors to be studied:
VI. Select the Experimental Design:
VII. Set Factor Levels:
VIII. Final Design Considerations:
nalyzing and Examining Result:
(i) Determine the parameters
signification (ANOVA)-Analysis of variance (Hafeez et.al 2002)
(ii) Conduct a main effect plot
analysis to determine the optimal level of the control factors.
(iii) Execute a factor contribution
rate analysis.
(iv) Confirm experiment and plan
future application
Conclusion:
Taguchi started to develop new
methods to optimize the process of engineering experimentation. He believed
that the best way to improve quality was to design and build it into the
product. He
developed the techniques which are
now known as Taguchi Methods. His main contribution lies not in the
mathematical formulation of the design of experiments, but rather in the
accompanying philosophy. His concepts produced a unique and powerful quality
improvement technique that
differs from traditional practices.
He developed manufacturing systems that were “robust” or insensitive to daily
and seasonal variations of environment, machine wear and other external
factors.
The Taguchi approach to quality
engineering places a great deal of emphasis on minimizing variation as the main means of improving quality. The
idea is to design products and processes whose performance is not affected by
outside conditions and to build this in during the development and design stage
through the use of experimental design. The method includes a set of tables
that enable main variables and interactions to be investigated in a minimum
number of trials. Taguchi Method uses the idea of Fundamental Functionality,
which will facilitate people to identify the common goal because it will not
change from case to case and can provide a robust standard for widely and
frequently changing situations. It is also pointed out that the Taguchi Method
is also very compatible with the human focused quality evaluation approach
(1) trial-and-error approach :
------------------------------
performing a series of experiments each of which gives some understanding. This requires making measurements after every experiment so that analysis of observed data will allow him to decide what to do next - "Which parameters should be varied and by how much". Many a times such series does not progress much as negative results may discourage or will not allow a selection of parameters which ought to be changed in the next experiment. Therefore, such experimentation usually ends well before the number of experiments reach a double digit! The data is insufficient to draw any significant conclusions and the main problem (of understanding the science) still remains unsolved.
(2) Design of experiments :
-----------------------------
A well planned set of experiments, in which all parameters of interest are varied over a specified range, is a much better approach to obtain systematic data. Mathematically speaking, such a complete set of experiments ought to give desired results. Usually the number of experiments and resources (materials and time) required are prohibitively large. Often the experimenter decides to perform a subset of the complete set of experiments to save on time and money! However, it does not easily lend itself to understanding of science behind the phenomenon. The analysis is not very easy (though it may be easy for the mathematician/statistician) and thus effects of various parameters on the observed data are not readily apparent. In many cases, particularly those in which some optimization is required, the method does not point to the BEST settings of parameters. A classic example illustrating the drawback of design of experiments is found in the planning of a world cup event, say football. While all matches are well arranged with respect to the different teams and different venues on different dates and yet the planning does not care about the result of any match (win or lose)!!!! Obviously, such a strategy is not desirable for conducting scientific experiments (except for co-ordinating various institutions, committees, people, equipment, materials etc.).
(3) TAGUCHI Method :
--------------------------
Dr. Taguchi of Nippon Telephones and Telegraph Company, Japan has developed a method based on " ORTHOGONAL ARRAY " experiments which gives much reduced " variance " for the experiment with " optimum settings " of control parameters. Thus the marriage of Design of Experiments with optimization of control parameters to obtain BEST results is achieved in the Taguchi Method. "Orthogonal Arrays" (OA) provide a set of well balanced (minimum) experiments and Dr. Taguchi's Signal-to-Noise ratios (S/N), which are log functions of desired output, serve as objective functions for optimization, help in data analysis and prediction of optimum results.
Taguchi Method treats optimization problems in two categories,
[A] STATIC PROBLEMS :
Generally, a process to be optimized has several control factors which directly decide the target or desired value of the output. The optimization then involves determining the best control factor levels so that the output is at the the target value. Such a problem is called as a "STATIC PROBLEM". This is best explained using a P-Diagram which is shown below ("P" stands for Process or Product). Noise is shown to be present in the process but should have no effect on the output! This is the primary aim of the Taguchi experiments - to minimize variations in output even though noise is present in the process. The process is then said to have become ROBUST.
[B] DYNAMIC PROBLEMS :
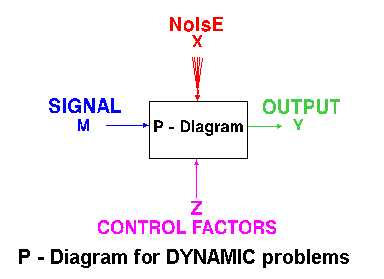
If the product to be optimized has a signal input that directly decides the output, the optimization involves determining the best control factor levels so that the "input signal / output" ratio is closest to the desired relationship. Such a problem is called as a "DYNAMIC PROBLEM".
This is best explained by a P-Diagram which is shown below. Again, the primary aim of the Taguchi experiments - to minimize variations in output even though noise is present in the process- is achieved by getting improved linearity in the input/output relationship.
[A] STATIC PROBLEM (BATCH PROCESS OPTIMIZATION) :
----------------------------------------------------------------------------
There are 3 Signal-to-Noise ratios of common interest for optimization of Static Problems; (I) SMALLER-THE-BETTER :
--------------------------------------
n = -10 Log10 [ mean of sum of squares of measured data ]This is usually the chosen S/N ratio for all undesirable characteristics like " defects " etc. for which the ideal value is zero. Also, when an ideal value is finite and its maximum or minimum value is defined (like maximum purity is 100% or maximum Tc is 92K or minimum time for making a telephone connection is 1 sec) then the difference between measured data and ideal value is expected to be as small as possible. The generic form of S/N ratio then becomes,n = -10 Log10 [ mean of sum of squares of {measured - ideal} ]
(II) LARGER-THE-BETTER :
-------------------------------------
n = -10 Log10 [mean of sum squares of reciprocal of measured data]
This case has been converted to SMALLER-THE-BETTER by taking the reciprocals of measured data and then taking the S/N ratio as in the smaller-the-better case.
(III) NOMINAL-THE-BEST :
-----------------------------------
square of mean
n = 10 Log10 -----------------
variance
This case arises when a specified value is MOST desired, meaning that neither a smaller nor a larger value is desirable.
Examples are;
(i) most parts in mechanical fittings have dimensions which are nominal-the-best type.
(ii) Ratios of chemicals or mixtures are nominally the best type.
e.g. Aqua regia 1:3 of HNO3:HCL
Ratio of Sulphur, KNO3 and Carbon in gun powder
(iii) Thickness should be uniform in deposition /growth /plating /etching..
[B] DYNAMIC PROBLEM (TECHNOLOGY DEVELOPMENT) :
------------------------------------------------------------------------------
In dynamic problems, we come across many applications where the output is supposed to follow input signal in a predetermined manner. Generally, a linear relationship between "input" "output" is desirable.
For example : Accelerator peddle in cars,
volume control in audio amplifiers,
document copier (with magnification or reduction)
various types of moldings
etc.
There are 2 characteristics of common interest in "follow-the-leader" or "Transformations" type of applications,
(i) Slope of the I/O characteristics
and
(ii) Linearity of the I/O characteristics
(minimum deviation from the best-fit straight line)
The Signal-to-Noise ratio for these 2 characteristics have been defined as;
(I) SENSITIVITY {SLOPE}:
----------------------------------
n = 10 Log10 [square of slope or beta of the I/O characteristics]
On the other hand, when the output is an undesired characteristics, it can be treated as Smaller-the-Better.
n = -10 Log10 [square of slope or beta of the I/O characteristics]
-----------------------------------------------
Most dynamic characteristics are required to have direct proportionality between the input and output. These applications are therefore called as "TRANSFORMATIONS". The straight line relationship between I/O must be truly linear i.e. with as little deviations from the straight line as possible. Square of slope or beta
n = 10 Log10 ----------------------------
variance
Variance in this case is the mean of the sum of squares of deviations of measured data points from the best-fit straight line (linear regression).
(4) 8-STEPS IN TAGUCHI METHODOLOGY :
---------------------------------------------------- Taguchi method is a scientifically disciplined mechanism for evaluating and implementing improvements in products, processes, materials, equipment, and facilities. These improvements are aimed at improving the desired characteristics and simultaneously reducing the number of defects by studying the key variables controlling the process and optimizing the procedures or design to yield the best results.
The method is applicable over a wide range of engineering fields that include processes that manufacture raw materials, sub systems, products for professional and consumer markets. In fact, the method can be applied to any process be it engineering fabrication, computer-aided-design, banking and service sectors etc. Taguchi method is useful for 'tuning' a given process for 'best' results.
Taguchi proposed a standard 8-step procedure for applying his method for optimizing any process,
8-STEPS IN TAGUCHI METHODOLOGY:
Step-1: IDENTIFY THE MAIN FUNCTION, SIDE EFFECTS, AND FAILURE MODE
Step-2: IDENTIFY THE NOISE FACTORS, TESTING CONDITIONS, AND QUALITY CHARACTERISTICS
Step-3: IDENTIFY THE OBJECTIVE FUNCTION TO BE OPTIMIZED
Step-4: IDENTIFY THE CONTROL FACTORS AND THEIR LEVELS
Step-5: SELECT THE ORTHOGONAL ARRAY MATRIX EXPERIMENT
Step-6: CONDUCT THE MATRIX EXPERIMENT
Step-7: ANALYZE THE DATA, PREDICT THE OPTIMUM LEVELS AND PERFORMANCE
Step-8: PERFORM THE VERIFICATION EXPERIMENT AND PLAN THE FUTURE ACTION
SUMMARY :
Every experimenter develops a nominal process/product that has the desired functionality as demanded by users. Beginning with these nominal processes, he wishes to optimize the processes/products by varying the control factors at his disposal, such that the results are reliable and repeatable (i.e. show less variations). In Taguchi Method, the word "optimization" implies "determination of BEST levels of control factors". In turn, the BEST levels of control factors are those that maximize the Signal-to-Noise ratios. The Signal-to-Noise ratios are log functions of desired output characteristics. The experiments, that are conducted to determine the BEST levels, are based on "Orthogonal Arrays", are balanced with respect to all control factors and yet are minimum in number. This in turn implies that the resources (materials and time) required for the experiments are also minimum.
Taguchi method divides all problems into 2 categories - STATIC or DYNAMIC. While the Dynamic problems have a SIGNAL factor, the Static problems do not have any signal factor. In Static problems, the optimization is achieved by using 3 Signal-to-Noise ratios - smaller-the-better, LARGER-THE-BETTER and nominal-the-best. In Dynamic problems, the optimization is achieved by using 2 Signal-to-Noise ratios - Slope and Linearity.
Taguchi Method is a process/product optimization method that is based on 8-steps of planning, conducting and evaluating results of matrix experiments to determine the best levels of control factors. The primary goal is to keep the variance in the output very low even in the presence of noise inputs. Thus, the processes/products are made ROBUST against all variations.


No comments:
Post a Comment